Activity 8: 3D Surface Reconstruction fron Structured Light

Three-dimensional (3D) imaging can be performed on an object with various methods. One can rotate the object and image the rotation or just image the object and rotate the camera. However, there are some instances that the object or camera rotation is impossible to perform. An alternative is by projecting grid illuminations on the object. It is observed that distortions on the grids appear whenever a flat surface is encountered. An example of this is shown in Figure 1 where various gray code patterns are projected on a pyramid.

Figure 1. Upper images: Gray grid patterns projected on a flat surface. Bottom images: Gray grid patterns projected on a pyramid.

The 3D image of the pyramid is generated from the bit plane stack (BPS). The BPS is just the sum of the gray patterns that are each multiplied by its bit weight. The bit weights for the seven grid patterns are from 2^0 to 2^6. The BPS of the flat surface and the pyramid are shown in Figures 2 and 3.

Figure 2. BPS of the flat surface.

Figure 3. BPS of the pyramid.

The 3D image is formed from the two BPS by obtaining the displacement of the stripes. The displacement is the actual height of the object. The 3D image of the pyramid is shown in Figures 4 and 5.

Figure 4. Sample 3D image of the pyramid.

Figure 5. Second sample 3D image of the pyramid shown at a different angle.

There are noise from the 3D image so filtering methods must be added to the 3D reconstruction process.

I give myself a grade of 10 for this activity.

I would like to acknowledge Thirdy for lending me the images of the grid patterns for the flat surface and the pyramid.

Reference:

[1] J.Guhring, "Dense 3D surface acquisition by structured-light using off-the-shelf components,".

Activity 5: Camera Calibration

Camera calibration is performed to determine image coordinates from the real world coordinates. There are two methods that can be used for camera calibration: (A) folded checkerboard and (B) camera calibration toolbox.

A. Using a Folded Checkerboard

An image of the folded checkerboard is shown in Figure 1 with the convention of the x, y, and z axes.

Figure 1. Folded checkerboard with axes convention.

25 Points are chosen from the folded checkerboard as shown in Figure 2. The selected points are some corners of the checkers from the folded checkerboard.

Figure 1. Selected 25 points in the folded checkerboard.

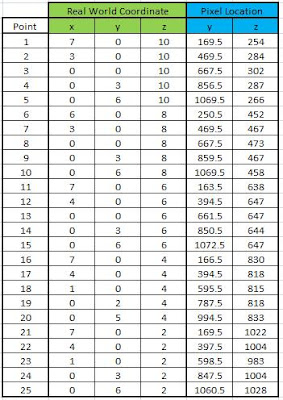
The real world and image coordinates of the chose points are given in Table I. The image coordinates are obtained via the ginput function of Matlab 7.

Table I. Real world and image coordinates of the 25 Points.

The camera parameters a are obtained from the real world and image coordinates using Equation 33 of Ref. 1. The predicted image coordinates using the camera parameters a are obtained using Equations 29 and 30 of Ref. 1. The predicted image coordinates are shown in Figure 2.

Figure 2. Predicted new image coordinates using the camera parameters.

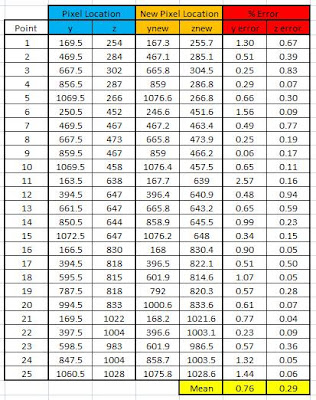
A comparison of the manually obtained and predicted image coordinates is given in Table II. It is observed that the mean errors for the y and z are 0.76 and 0.29, respectively. The small error indicates that camera calibration technique performs properly.

Table II. Comparison of the manually obtained and predicted image coordinates.

The camera calibration is again tested finding all the point in the z axis. The predicted image coordinates using the camera parameters are shown in Figure 3.

Figure 3. Predicted image coordinates found in the z axis.

B. Using the Camera Calibration Toolbox

Another method for camera calibration is through a toolbox developed for Matlab. The toolbox can be downloaded from Ref. 2. 20 images of a checkerboard with various translations and rotations are needed for this method. The 20 images are shown in Figure 4.

Figure 4. Images of a checkerboard under various translations and rotations.

Using the toolbox, the Matlab GUI will ask to point the edges of the checkerboard. The image with the chosen edges of the checkerboard is shown in Figure 5.

Figure 5. Selected edges of the checkerboard.

After selecting the edges of checkerboard, the toolbox will ask the user to confirm whether the corners of the checkerboard are all detected. The predicted corners of the checkerboard are shown in Figure 6 for some of the translations and rotations.

Figure 6. Predicted corners of the checkerboard for some translations and rotations.

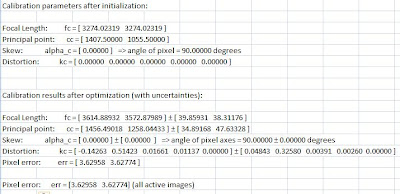
The intrinsic parameters such as the focal length, skew, etc. are outputs of the toolbox. The intrinsic parameters are given in Table III.

Table III. Intrinsic parameters.

The extrinsic parameters such as the translations and rotations of the checkerboard with respect to a camera location (camera-centered) are shown in Figure 7.

Figure 7. Checkerboard translations and rotations with respected to a camera location.

The extrinsic parameters such as the camera locations with respect of the checkerboard position (checkerboard-centered) are shown in Figure 8.

Figure 8. Camera locations with respect to a checkerboard position.

I give myself a grade of 10 for this activity.

References:

[1] M. Soriano, A Geometric Model for 3D Imaging, 2009.

[2] http://www.vision.caltech.edu/bouguetj/calib_doc.